You hear your name and it should appear on the board – these are not necessarily the best memories of school. Fortunately, I survived the helpless guesswork in front of the class. But maybe you would solve the task on the board with flying colors?
It’s the squares of numbers 1 .2 up to 1002. Find the sum of all even square numbers and subtract the sum of all odd square numbers.
What is the result of the calculation?
the result is 5050. This is exactly the sum of all numbers from 1 to 100.
Finding the solution is not particularly difficult when we have binomial formula
a2 – B2 = (a – b) * (a + b)
use.
We rearrange the squares – in descending order of size – and add the corresponding sign in each case – that is, plus or minus:
Total = 1002 – 992 +982 – 972 + … + 22 – 12
We now rewrite the differences between two square numbers using the binomial formula:
Total = (100-99) * (100 + 99) + (98-97) * (98 + 97) + … + (2-1) * (2 + 1)
Since adjacent numbers always differ from exactly 1, we can simply omit the expressions (100-99), (98-97) and so on. This greatly simplifies the calculation:
Total = 100 + 99 + 98 + 97 + … + 2 + 1
We don’t have to add the numbers from 1 to 100 in our heads, we use the trick with which the mathematician Carl Friedrich Gauss once impressed his teacher as a student. To do this, we simply rearrange the numbers into 50 pairs, totaling 101 for each pair:
Sum = (100 + 1) + (99 + 2) + … + (51 + 50)
Total = 50 * 101 = 5050
If you missed a puzzle from the past few weeks, here are the last ten episodes:

“Total coffee aficionado. Travel buff. Music ninja. Bacon nerd. Beeraholic.”






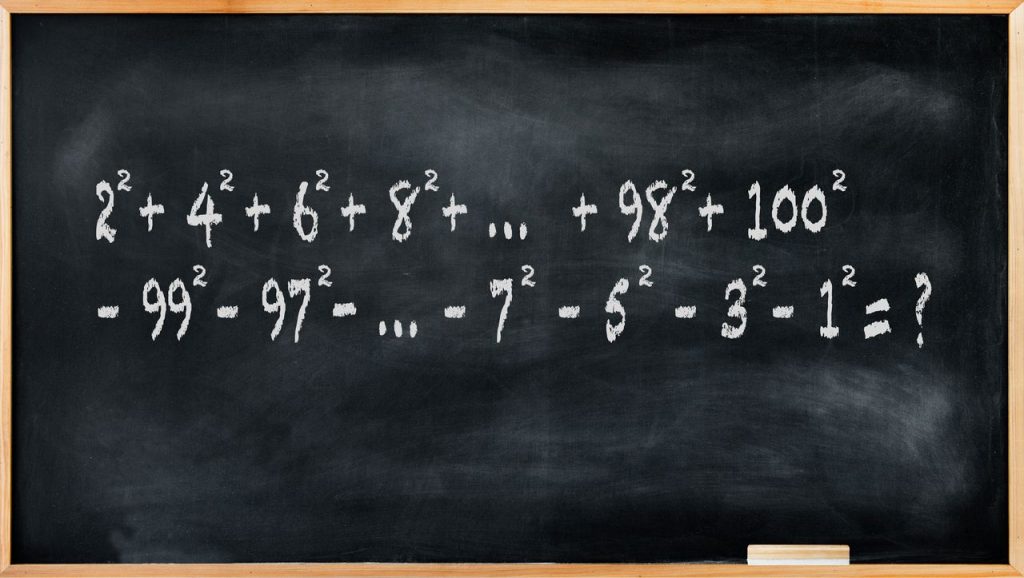
More Stories
Exploding Fireball: Find the meteorite fragments
Neuralink's competitor lets blind people see again with an implant
A huge meteorite has hit Earth – four times the size of Mount Everest